Uttryck, ekvationer och olikheter
a) Hantering av matematiska uttryck
Förmåga att hantera matematiska uttryck har visat sig vara viktigt för utveckling av algebraiska tänkandet. I Finland lär sig barn redan i åk 1 att formulera och tolka uttryck som ”2 + 3” eller ”5 – 2” med hjälp av konkreta medel och problem från deras närmiljö eller sagovärld. Traditionellt har det i det finländska läromedlet ansetts vara viktigt att skriva ett uttryck för lösningar av textproblem och inte enbart visa beräkningar och svar. Det är bra att fortsätta med det! I Finland, till skillnad från Sverige, får barnen också tidigt lära sig att formulera mer komplicerade uttryck som kräver kunskap om prioriteringsöverenskommelser och användning av parenteser. Till exempel i Sverige har man traditionellt infört detta först på högstadiet. Det finns dock något viktigt som ofta saknas i finländska matematikläroböcker. Det handlar om att utgå från ett uttryck och fundera på vilket problem det kan vara en lösning till. Detta hjälper barnen att utveckla intuitiv förståelse för generaliteten av matematiska uttryck. Samma uttryck är lösning till olika problem. Sådana övningar har vi hittat i både svenska och estniska läromedel. Hannele Ikäheimo har producerat övningar där barn lär sig att starta från ett matematiskt uttryck, ett problem eller en konkret bild, vilket kan användas som inspiration för lämpliga aktiviteter som ökar barnens förståelse för matematiska uttryck. (se på finska http://opperi.fi/02_opetusvinkkeja/2211_tarinapaperi.html)
b) Ekvationer
Ekvationer och olikheter kan man börja arbeta med barnen från åk 1 och även tidigare i konkreta situationer och i början utan matematiska symboler för tal. Man kan arbeta helt retoriskt med konkreta medel.
Ekvationslösning i nybörjarundervisningen syftar inte till användning av formella metoder som elever traditionellt lärt sig under senare skolåren även om det kan utvecklas en intuitiv förståelse till dem, utan informella metoder. Det kan handla om testandet med olika tal som gör en likhet sann eller olika typer av logiska slutledningar. I många länder lär sig barnen att lösa enkla ekvationer genom att utnyttja motsatta operationer. Detta förekommer också i några finländska läromedel. Till exempel kring ekvationen _ – 4 = 6 lär barnen att med konkreta medel förstå att man från början haft en okänd mängd någonting och efter att gett bort 4 har 6 kvar. Då kan de lätt lära sig att tänka att de tar tillbaka 4 och då får de se hur mycket de hade från början. Att utnyttja sambandet mellan addition och subtraktion, samt multiplikation och division är en viktig förmåga att utveckla hos barnen. Ytterligare en till informell metod är att man räknar baklänges.
Det finns ett särdrag framför allt i finska läromedel där man från första början hittar uppgifter där elever ska med logisk slutledning nysta fram en lösning till ett ekvationssystem. Det är också mycket bra förberedelse innan de lär sig mer formella metoder att lösa ekvationssystem på senare skolåren.
Bild 3. Ekvationssystem som elever kan lösa med informella metoder
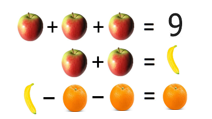
c) Olikheter
Med olikheter kan man arbeta parallellt med likheter och ekvationer. Bra att först börja med jämförelser av tal. Det går utmärkt att arbeta konkret med likhetstecknet och mindre än/större än tecknet. Barnen brukar få sådana tecken tillsammans med sifferkort i kuvert som medför matematikboken. Symboler kan man arbeta med parallellt med konkret material som klossar, bönor eller liknande. Så småningom kan man till och med börja jämföra uttryck. Barnen kan också fundera på med vilka variabelvärden den ena uttrycken är större/mindre än det andra. När är de lika?
Likhetstecknets betydelse
Likheter och olikheter är starkt kopplat till barnens förståelse av antals-begreppet, t ex att tre myror är flera än två elefanter. Att barnen från första början utvecklar förståelse för likhetstecknets betydelse är viktigt för algebraiskt tänkande och förståelse av ekvationer. I många finländska läromedel är det vanligt att parallellt med likhetstecken lära sig tecknen för olikheter (”mindre än” < , ”större än” > och ”lika med” =). I början jämför man antal, så som antalet myror och elefanter och barnen får sätta ett rätt tecken i dessa jämförelser. Men redan i åk 1 går det alldeles utmärkt att börja jämföra även uttryck, t ex 2 + 3 _ 3 + 2.
När det gäller likhetstecknets betydelse, menar forskare att det för ofta förknippas med ett svar på en operation (operationell betydelse). Risken är stor om elever enbart möter likhetstecknet i samband med beräkningar som 8 – 5 = 3. Så är fallet med många finländska läromedel. Om man dessutom läser det som 8 – 5 ”blir” 3 i stället för 8 – 5 ”är lika med” så tonar man ännu mera ner likheten mellan två sidor av tecknet (strukturell betydelse). I svenska läromedel för åk 1-2 är situationen det motsatta. Så kallade öppna utsagor t ex ”3 + _ = 8 – _” dyker upp innan barnen lärt sig förstå aritmetiska operationer och deras sinsemellan kopplingar, vilket kan i många fall leda till olika typer av missuppfattningar som är svåra att senare reda ut. Det är viktigt att införa arbetet med ekvationer på ett genomtänkt sätt.
Läs mer om hur man arbetat med likhetstecknet i åk 1 i Davydov-andan i artikeln som du hittar här: https://forskul.se/ffiles/006F5514/FUL10_Algebra.pdf
