Grekernas talvärld bestod av geometriska objekt som sträckor och rektanglar. De hade ett antalsbegrepp men inga reella tal. Sträckor kunde multipliceras och resultatet blev en rektangel. Produkten av tre sträckor blev ett rätblock, men multiplikation av fyra sträckor kunde inte utföras. Ekvationslösning beskrevs i geometriska termer, vilket också kallas geometrisk algebra. Ett typiskt sådant exempel är följande.

Problem. Tre sträckor a, b och c är givna. Sökt är en sträcka x så att rektangeln med sidorna b och c är lika stor som rektangeln med sidorna a och x.

Idag skulle vi lösa problemet genom att mäta sträckorna a, b och c och få tre reella tal, som vi också betecknar med a, b och c. Längden av sträckan x får vi genom att vi först multiplicerar sträckorna b och c och sedan dividerar resultatet med a. Då blir de två rektanglarna lika stora eftersom a multiplicerad med x blir arean av den ena rektangeln och produkten av b och c blir arean av den andra rektangeln.

Hur löste grekerna problemet utan att använda sig av längder och areor? Som ofta är fallet med geometriska problem, så består lösningen av en genial konstruktion följd av ett likaså genialt bevis för att konstruktionen är korrekt.

Konstruktion
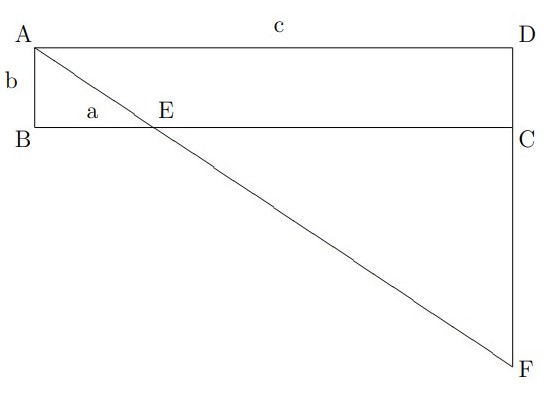
Avsätt sträckan a, som vi antar är kortare än c, på sträckan BC med början vid B. Låt E vara högra ändpunkten av sträckan a. Dra AE och förläng den tills den skär förlängningen av CD. Låt F vara denna skärningspunkt. Den sökta sträckan x är då DF.

Bevis
För att bevisa att DF är den sökta sträckan, fullborda rektangeln ADFG och dra en linje genom E parallell med DF. Denna linje skär GF i punkten H och AD i punkten I.

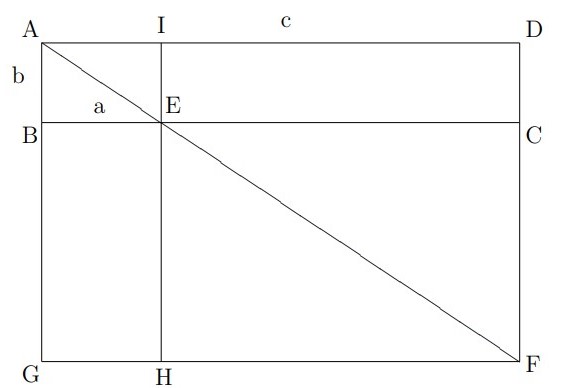Eftersom sträckan DF är lika med sträckan AG så gäller det att bevisa att rektangeln AGHI är lika stor som rektangeln ABCD. Men triangeln GAF är lika med triangeln DFA eftersom båda är rätvinkliga och har lika långa sidor. På samma sätt är trianglarna BAE och IEA lika och även trianglarna HEF och CFE. Härav följer att rektanglarna BGHE och IECD är lika stora enligt principen att om man subtraherar lika mycket från två lika storheter så blir
återstående delar lika. Genom addition av lika storheter får man till slut att rektanglarna AGHI och ABCD är lika stora.

Texterna och uppgifterna om algebrans historia och geometrisk algebra är skrivna av professor emeritus Clas Löfwall.